开个新坑,games101
Part 1
计算机视觉和计算机图形学的区别。
一切需要猜测的东西,是CV 。 需要理解。
那里是马路,那里是斑马线
MODEL -> IMAGE 图形学
IMAGE -> MODEL CV
IMAGE -> IMAGE CV
MODEL -> MODEL 图形学
难道两者结合起来不能作为一个方向吗?为什么要区分的这么严格。
Part 2
主要了解,向量的点积和叉积。
点积:又称标量积,内积
两个向量的点积结果是一个数,规则就是对应元素相乘。
\[\mathbf{a} = \begin{bmatrix} a_1 \\ a_2 \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix}, \quad \mathbf{a} \cdot \mathbf{b} = a_1 \times b_1 + a_2 \times b_2\]对应元素相乘,这就是点积。
叉积:$\mathbf{a}、\mathbf{b}$两个向量作叉积,结果是$\mathbf{c}$向量,并且$\mathbf{c}$向量垂直于$\mathbf{a}、\mathbf{b}$向量。
\[\mathbf{a} \begin{bmatrix} a1 \\ a2 \\ a3 \end{bmatrix} , \ \ \mathbf{b} \begin{bmatrix} b1 \\ b2 \\ b3 \end{bmatrix} \\ \mathbf{a} \times \mathbf{b} = \left| \begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a1 & a2 & a3 \\ b1 & b2 & b3 \\ \end{array} \right|\]我们默认在计算机图形学中使用右手系法则。
我们可以用右手定则在叉积中的应用来判断,一个点在一个平面的外部还是内部。
Part 3
开始慢慢涉及到变化,内容开始变多。
首先学习2D的rotation、scale和shear。
Scale
把一个图形,等比例缩放。
对于上述公式,我们可以写成矩阵形式
\[\begin{equation} \begin{bmatrix} x{\prime} \\ y{\prime} \end{bmatrix} = \begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \end{equation}\]当然,缩放可以不按相同的比例。
Reflection Matrix
下面看一个常用的反射矩阵
对此,我们可以得到 \(\begin{equation} \begin{bmatrix} x{\prime} \\ y{\prime} \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \end{equation}\)
shear Matirx
我们可以看到,上图中,矩形被拉伸了。那我们该如何写出变换矩阵呢,我们要抓住不动量。
- 整个图形,$y$轴上的值没有变化,因此 $ y = y{\prime} $
- 在观察$x$轴的变化,随着$y$值得变化,对应的x也相应得产生了便宜。当$y = 1$时, $x = a$; $y = 0$时,$x = 0$;
由此,我们可以推理出:
\[\begin{equation} \begin{bmatrix} x{\prime} \\ y{\prime} \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \end{equation}\]Rotation Matrix
这里公式太多用Latex写太麻烦了,我就直接贴原PPT图片了。对于把一个图形,绕着原点旋转$\theta(0 \leq \theta < 90)$,可以用上述矩阵表示,但不需要记住,因为可以现场推演。
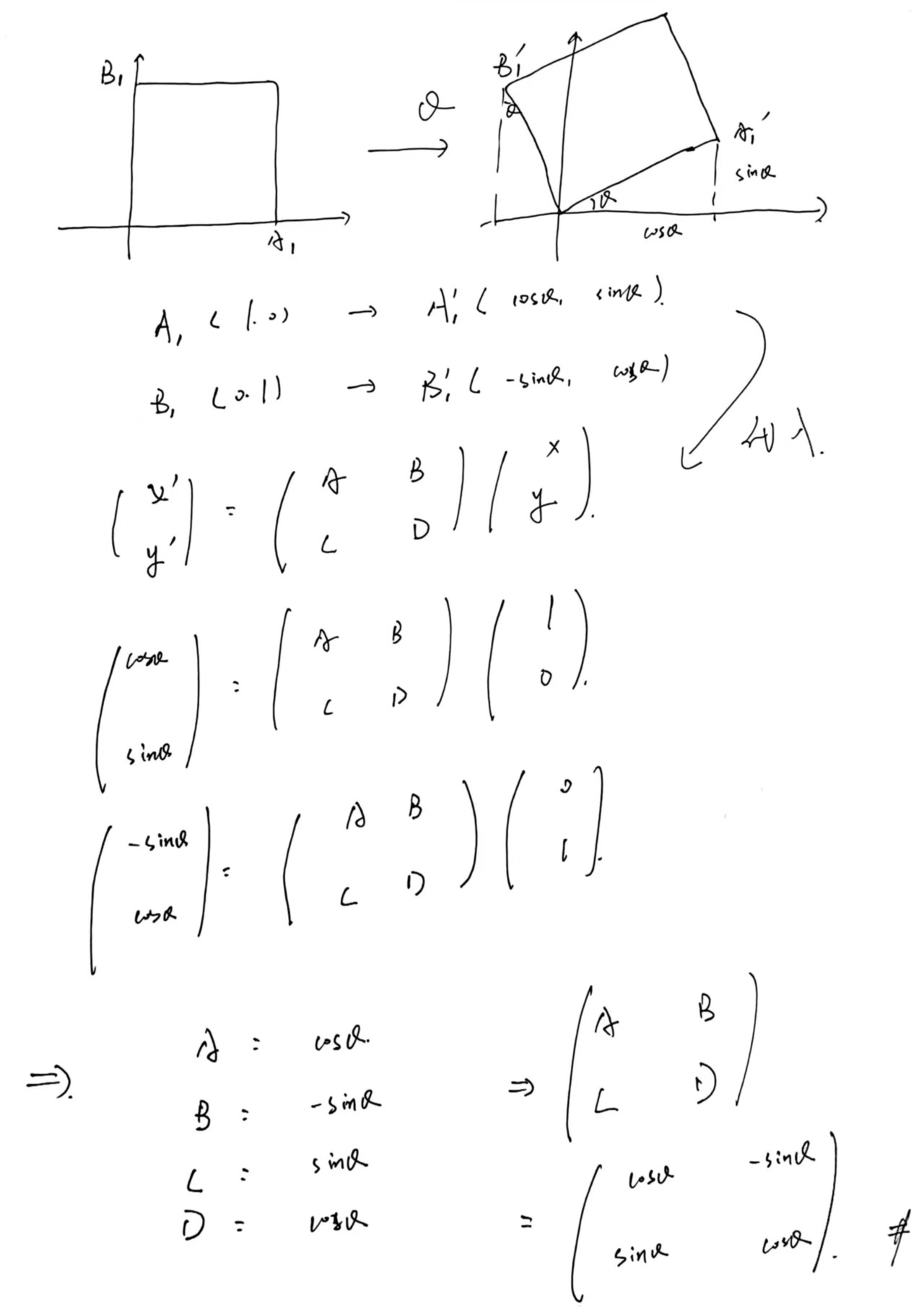
上述几个例子,我们可以得到,线性变化我们都可以使用矩阵来表示。但是如果,图形进行平移变化呢?我们是否还是简单的用矩阵表示。
Traslation
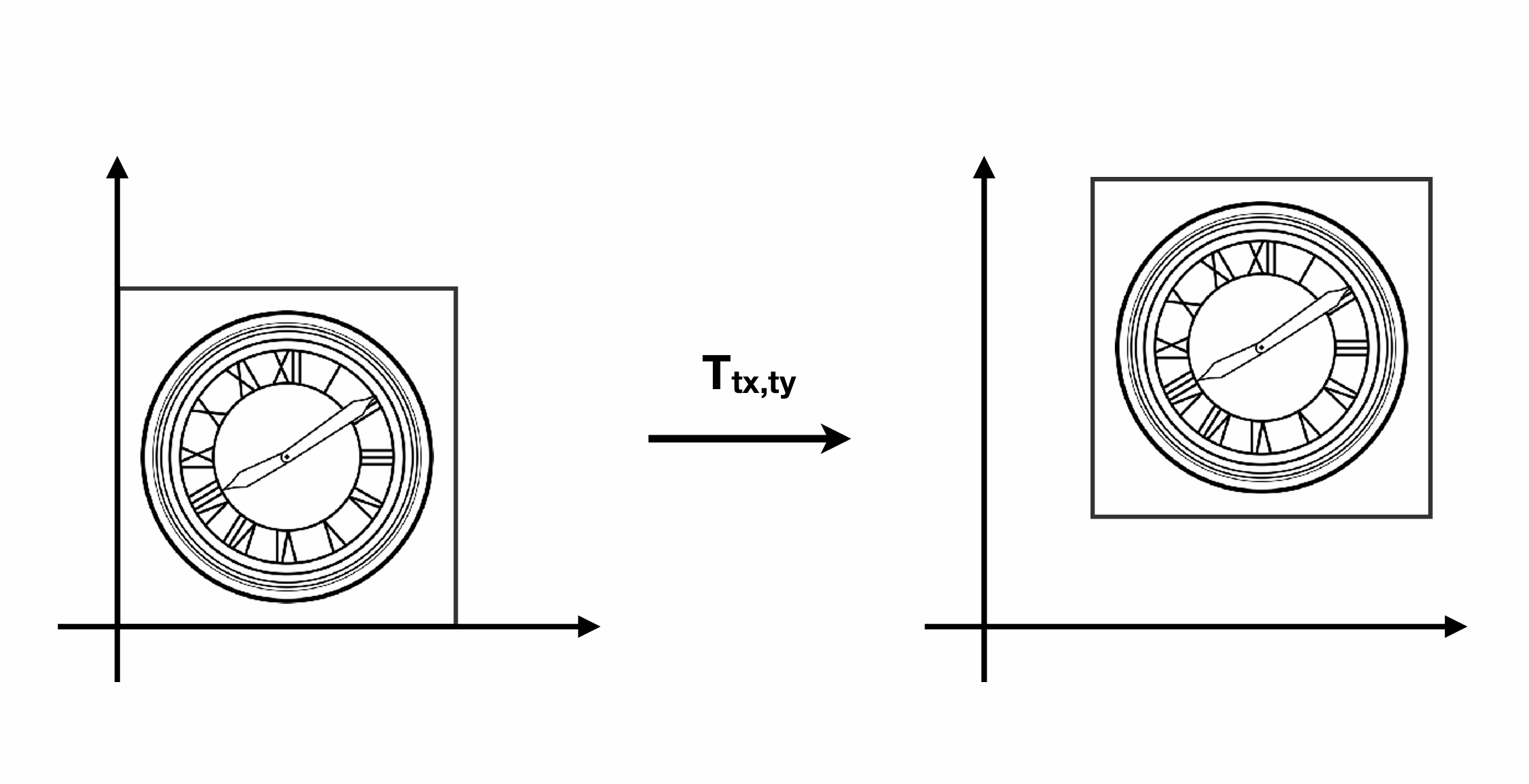
这里我们将图形进行了$x$和$y$轴上的平移。
\[x{\prime} = x + t_x, \ y{\prime} = y + t_y \\\]此时:
\[\begin{equation} \begin{bmatrix} x{\prime} \\ y{\prime} \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} \end{equation}\]我们会发现,平移变化和缩放,旋转变化不一样。那能不能把几个不同的变化统一成一种形式?
由此,我们引入,齐次坐标的概念。
齐次坐标:通过N+1维坐标来表示N维坐标。
我们通过,对二维坐标系增加一维的方法来统一不同的变化矩阵。
$2D \ point = (x, y, 1)^T$
$2D \ vector = (x, y, 0)^T$
由此上述的平移变化,我们可以写成:
\(\begin{bmatrix}
x{\prime} \\
y{\prime} \\
w{\prime}
\end{bmatrix}
=
\begin{bmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
1
\end{bmatrix}
=
\begin{bmatrix}
x + t_x \\
y + t_y \\
1
\end{bmatrix}\)
为什么,增加的那一维,点用0,向量用1呢?
很简单,我们可以回忆一下
空间中,一个点,减去另一个点,得到的是不是向量。一个向量减去另一个向量还是向量吧。所以很好理解,后缀到底是1还是0。
这样,我们就统一了各种变化,不光伸缩,平移还是旋转都可以使用齐次坐标来统一表示。
例如 Scale
\[S(s_x, s_y) = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{bmatrix}\]讲完了,单一的变化,如果各种变化结合起来,我们应该怎么分析呢?
不管什么变化组合,我们都先将它平移到原点进行一系列变化,变化完成后再逆着平移回要求的点处。
三维同理。
Part 4
3D的变化分为两大类,都是不同角度从三维变为二维的一张图。
- View transformation(视图变化,观测)
- Projection transformation(投影变化)
- Orthographic(正交)
- Perspective(透视)
结合上一讲,我们使用齐次坐标来表示三维的点和向量。
$3D \ point = (x, y, z, 1)^T$
$3D \ vector = (x,y,z,0)^T$
三维的所有仿射变化都可以用一个四维的矩阵来表示。什么叫仿射变化,线性变化和平移变化的叠加。下面是三维的点。
\[\begin{bmatrix} x{\prime} \\ y{\prime} \\ z{\prime} \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]我们单独看三维的旋转,我们默认不管二维还三维,旋转都是逆时针。
然后,我们回顾,二维的旋转变化。
我们发现,以哪根轴为中心,进行旋转对应的值不变。
例如:围绕x轴转,x的坐标都不会改变,旋转的矩阵也跟二维一样。但y轴会有点特殊。这是由于zx的右手系,才能得到y,又
\[\begin{align*} R_\theta &= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \\ R_{-\theta} &= \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} = {R_\theta}^T \\ R_{-\theta} &= {R_\theta}^{-1} \end{align*}\]View transformation
what is view transformation ?
MVP:
- model:搭好场景
- view:找一个好的视角
- projecting:3D投影到2D
在空间中,我们假设有一个出现在随机位置的摄像机,我们可以得知它的位置,它的摄影方向,它的摆放位置(正的放,倒的放)。
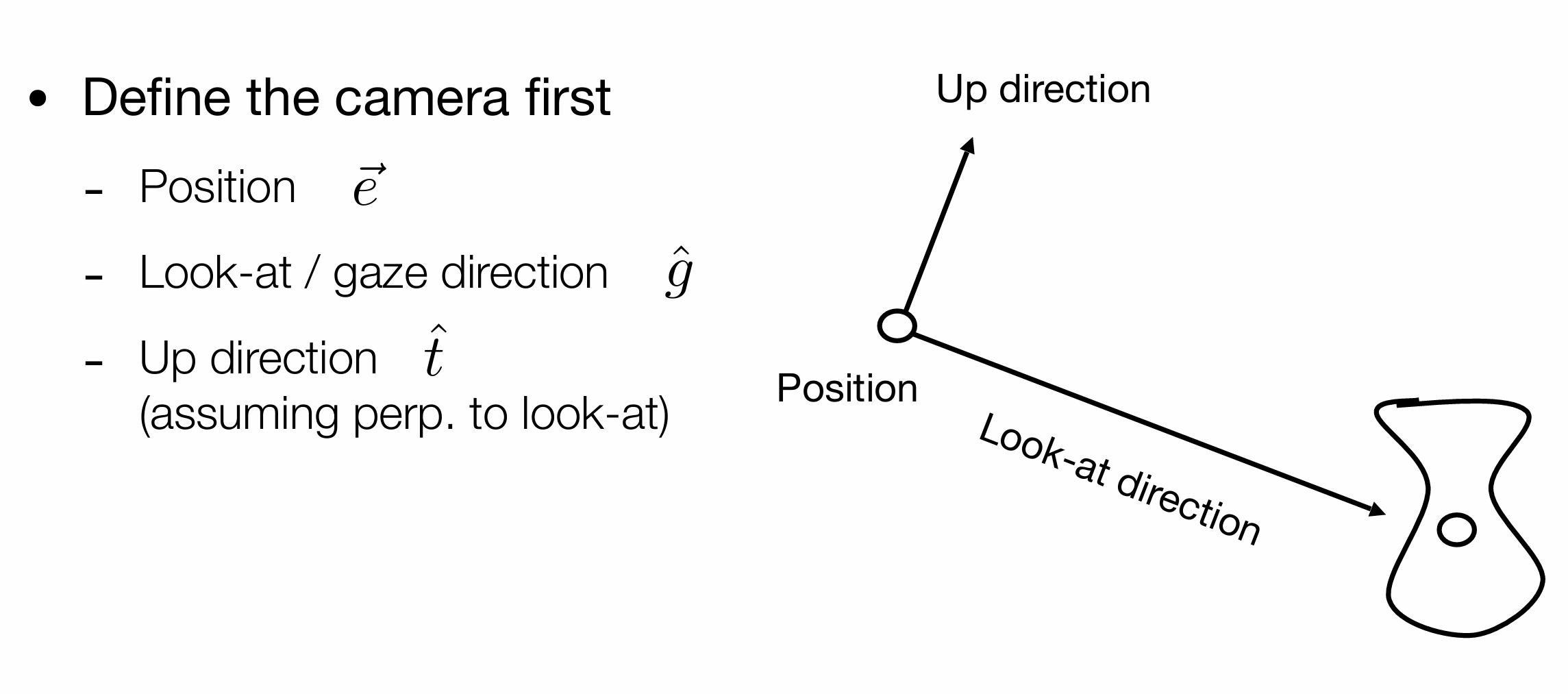
但是在空间中,我们这样去了解物体有点麻烦,我们决定,先整体移动到原点,再将$g$对准$-z$轴,$t$对准$y$,$g \times t$对准$x$。(因为整体做相对运动,视图不会变,为什么去原点,可以让操作简化,约定俗成。)
$M_{view} = R_{view}R_{view}$
具体操作,我写在了纸上。
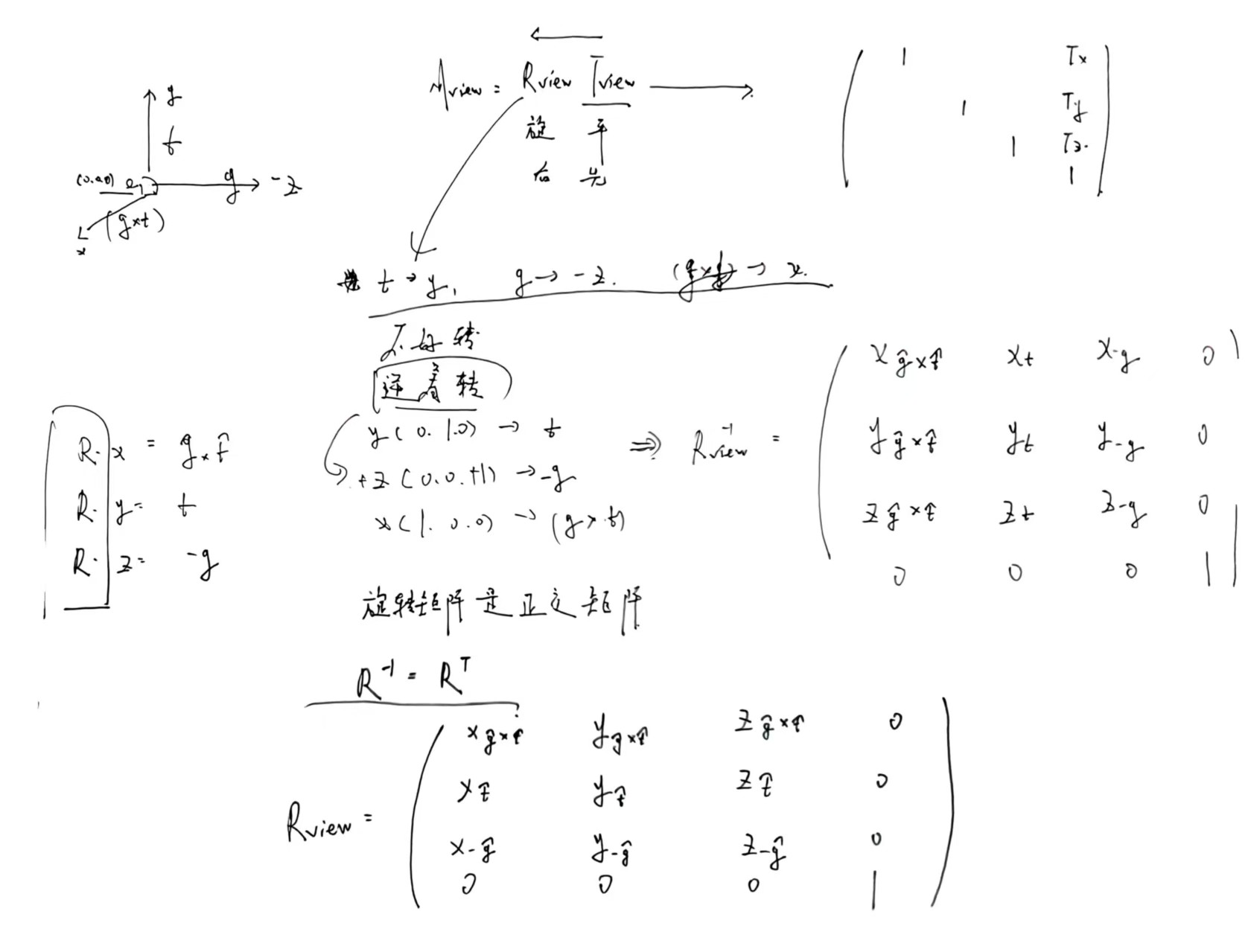
其中注意,旋转矩阵都是正交矩阵,正交矩阵的逆就是他自己的转置矩阵。其次,我们看左侧,这个$R_{view}$ 其实就是求一个变化矩阵
\[\begin{bmatrix} x{\prime} \\ y{\prime} \\ z{\prime} \\ \end{bmatrix} = R_{view} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}\]这个变化矩阵,不用深究,是已知的,初学不要去想怎么来的。
Projection transformation
Orthographic projection (正交投影)
Perspective projection (透视投影)
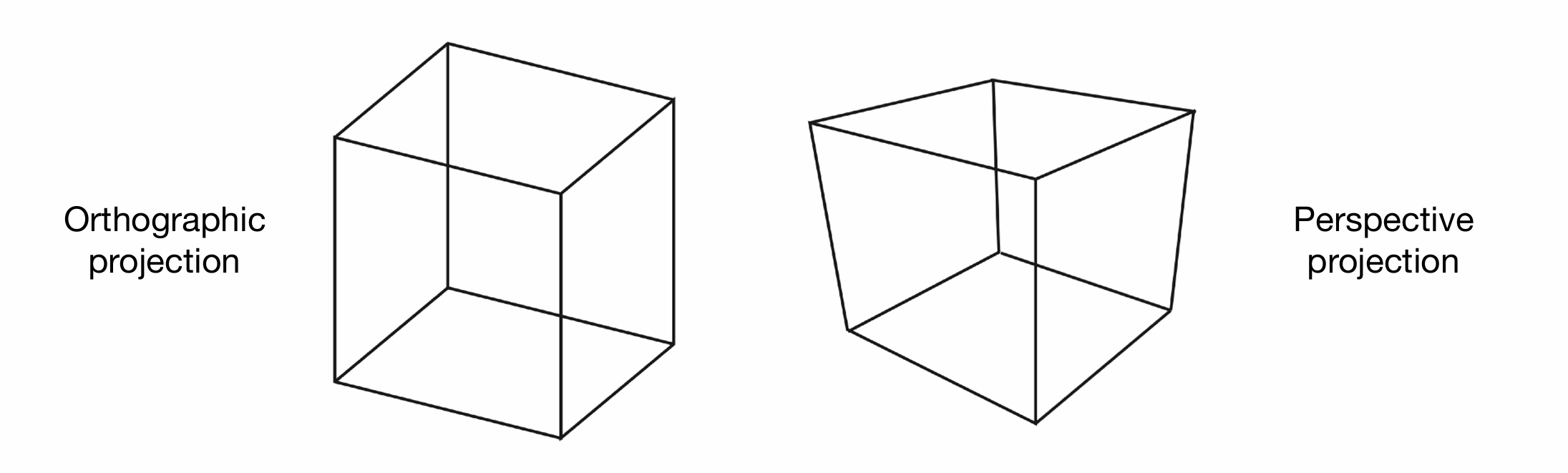
我们发现,正交投影,就跟我们画工程制图一样,十分的工整。但透视投影,明显更符合显示生活中,我们观察的场景,即平行线,却可以相交在某一点。
那我们引入这两种投影有什么用呢,具体怎么在坐标轴上操作投影呢?
回答问题1:
- 个人理解,不管是正交投影还是透视投影,都是为了我们把三维世界“压缩”到二维屏幕上,但不同的需求导致了两种不同的压缩方式。
- 最终世界是二维的,我们需要某种法则,进行统一,简便地映射。
- 不同场景,用到的投影肯定不同,机械相关的工程图,肯定使用正交投影。但有时候,我们需要呈现人眼的景象,这时候我们就需要使用透视投影。
- 三维,到二维并不是放弃了某一个维度。恰恰相反,我们可以人为规定,其中一个维度的方向。譬如$z$轴的方向。
问题2的回答,下面慢慢解释。
正交投影,如何进行?
- 我们从$z$轴,看整个物体
- 压缩$z$轴
- 把物体伸缩到$x$和$y$轴的[-1, 1]的正方形中
来看一个普遍的变化。
我们在三维空间中有随意的一个物体,我们改怎么进行正交投影呢?
- 首先把中心移动到原点处
- 压缩边长到[-1, 1]的范围内
来看如何用矩阵表示呢? 记住:先平移原点,后压缩
\[M_{ortho} = \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & 0 \\ 0 & \frac{2}{b - t} & 0 & 0 \\ 0 & 0 & \frac{2}{n - f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 & -\frac{r + l}{2} \\ 0 & 0 & 0 & -\frac{b + t}{2} \\ 0 & 0 & 0 & -\frac{n + f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}\]为什么平移前要加负号呢?
简单的带入数字,或者抽线的理解一下。在各个轴的正向,就往负方向平移,相反同理。
ok,接下来来讲透视投影。
透视投影,怎么进行?
我们将近大远小的物体先放缩成,长方体(n->n, f->f)。在进行正交投影。
遵守三个原则
- 近平面不动
- 最远的相对位置不动($z$轴不动)
- 远平面的中心点不动
这时候,我们能够观察到侧面,其实是一个相似三角形的放缩。
此时,空间任意一点
\[\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ unknow \\ 1 \end{pmatrix} == \begin{pmatrix} nx \\ ny \\ unknow \\ z \end{pmatrix} \\\]这是依赖,空间中任意一点,同时乘以不为0的数,还是表示同一个点。
所以,我们来看,原图形经过压缩,变为当前的点
\[M_{persp->ortho} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} nx \\ ny \\ unknow \\ z \end{pmatrix}\]推测出:
\[M_{persp->ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ \text{?} & \text{?} & \text{?} & ? \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}\]下面,我们依靠之前讲过的原则推断第三行的未知量。
近平面的点,在变化过程中不变,这里我们用n代替z
\[\\ \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} \Rightarrow \begin{pmatrix} nx \\ ny \\ n^2 \\ n \end{pmatrix} \\\]推测出未知的第三行
\[\begin{align*} \begin{pmatrix} 0 & 0 & A & B \end{pmatrix} \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} &= n^2 \\ \Rightarrow\quad An + B &= n^2 \end{align*}\]任何在最远平面的z轴不变 ,直接取最简单的点
\[\begin{pmatrix} 0 \\ 0 \\ f \\ 1 \end{pmatrix} \equiv \begin{pmatrix} 0 \\ 0 \\ f^2 \\ f \end{pmatrix} \Rightarrow Af + B = f^2\]解出:
\[\begin{align*} A &= n + f \\ B &= -n \end{align*}\]最后得到:
\[M_{persp->ortho} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & A & B \\ 0 & 0 & 1 & 0 \\ \end{pmatrix}\]A,B上方直接带入即可。
\[M_{persp} = M_{ortho}M_{persp->ortho}\]总结,透视投影就是先做一个长方体化,然后正交投影。结果就是透视投影